Getting Started
After installing the package you can run the first
FD script by executing
cd /your/path/to/FD/
xmaple
and then executing the following maple command:
read("fd_first_run.mpl");
which computes the FDA to the following derivatives:
$$
\frac{\partial^2 f(x)}{\partial x^2}
$$
$$
\frac{\partial^3 f(t,x,y)}{\partial t \partial x^2}
$$
Then by taylor expanding the FDA it confirms that the computed
expressions are accurate.
The output of your maple run should look like this:
| Warning, grid_functions is not assigned |
| FD table updated, see the content using SFDT() command |
| > |
B:=convert(series(B,hx),polynom); |
| > |
test_resid := simplify(eval(B-expr,{hx=0})); |
Computing df(t,x,y)/dtdx^2 using 2nd order forward in time and
centered in x scheme:
| > |
Update_FD_Table(2, table([ t=[0,-1],x=[-1,-1],y=[-1,-1],z=[-1,-1] ]) ); |
| FD table updated, see the content using SFDT() command |
| > |
expr:=diff(f(t,x,y),t,x,x); |
| > |
for ii from 1 to nops(stps) do |
| > |
B:=convert(series(B,stps[ii],4),polynom): |
| > |
test_resid := simplify(eval(B-expr,{ht=0,hx=0,hy=0})); |
The files fd_first_run.mpl and fd_first_run.mw are in the FD's
main
directory that you downloaded. Feel free to contact
Arman Akbarian
if you have any trouble starting to use FD.
See the tutorials section for more examples on posing
a PDE and solving it using FD.
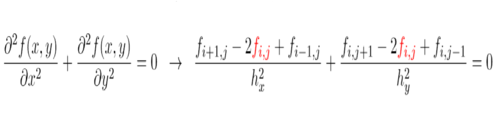
 FD: Finite Difference Toolkit in Maple
FD: Finite Difference Toolkit in Maple