Features
- Provides a simple syntactic language to specify a PDE and its boundary
conditions over a discretized numerical domain (Using a derived Maple
data structure: Discrete Domain Specifier
DDS)
- Creates Fortran routines and C wrappers for a given
DDS that
can evaluate an FDA expression or solve it
using Newton-Gauss-Seidel iterative method (commonly used for non-linear PDEs)
- Allows user specified discretization scheme such as
forward, backward, centered or asymmetric discretization
with used-defined accuracy via a data type (Maple table): Finite Difference Specifier,
FDS.
- Can handle various boundary conditions such as periodic boundary, inner
boundary conditions (imposing specific symmetry on the functions such as
even or odd behaviour on axis/point of symmetry) or other types of user
specified conditions, such as particular asymptotic behaviour,
outgoing (Neumann), fixed (Dirichlet), etc.
- Generates finite difference approximation of an arbitrary partial differential
expression of up to 4 variables,
f(t,x,y,z), for a used defined accuracy
and discretization scheme.
- Creates parallel ready Fortran routine that can interface with parallelization
infrastructures such as PAMR
- Can parse a given continuum algebraic/differential expression and can convert it directly to a
Fortran routine to evaluate it on the discretized domain. Doing so, it
provides a rapid prototyping language to create residual evaluators for
a given differential expression for testing purposes.
- Allows manual overwrite of discretization scheme by creating
Manual Finite Difference Operators defined via the built-in fundamental difference
operator.
- Mainly designed with a focus on highly complex and non-linear time dependent PDEs
or boundary value PDEs that occur in physical systems.
- It is written in Maple, a powerful symbolic manipulation language and
therefore inherits all the capabilities of Maple, including various tools
to deal with PDEs and algebraic expressions.
- It was originally developed in Numerical Relativity
group
 in UBC to solve the Einstein's equation which
is a set of 10 highly non-linear coupled PDEs, where even writing down the
equations in their continuum form needs to be done using symbolic
manipulation software such as GRTensor
in UBC to solve the Einstein's equation which
is a set of 10 highly non-linear coupled PDEs, where even writing down the
equations in their continuum form needs to be done using symbolic
manipulation software such as GRTensor  .
Therefore it is mostly developed to deal with large differential expressions
that are machine generated and carries a full explicit form with all the
dependencies and derivatives written in Maple's canonical form like:
.
Therefore it is mostly developed to deal with large differential expressions
that are machine generated and carries a full explicit form with all the
dependencies and derivatives written in Maple's canonical form like:
diff(f(t,x,y),x,x)+g(x,y)+diff(g(x,y),y,y,y)+...
- Being a Maple toolbox, FD unifies the two parts
of: (1)deriving and manipulating the set of PDEs
with all the required work variables, and (2) converting them
into FDA expression and solving them. This can further help to reduce potential human errors.
last update: Sun May 08 2016
in UBC to solve the Einstein's equation which is a set of 10 highly non-linear coupled PDEs, where even writing down the equations in their continuum form needs to be done using symbolic manipulation software such as GRTensor
. Therefore it is mostly developed to deal with large differential expressions that are machine generated and carries a full explicit form with all the dependencies and derivatives written in Maple's canonical form like:
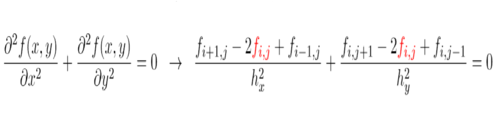
 FD: Finite Difference Toolkit in Maple
FD: Finite Difference Toolkit in Maple